
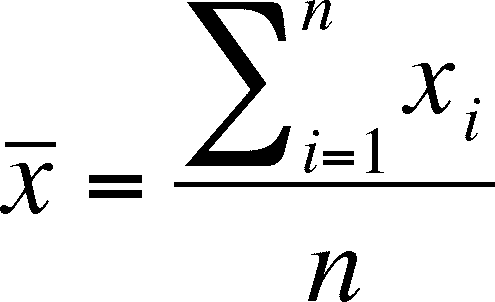
This allows statisticians to identify any outliers in their data so they can adjust their data accordingly when their well-controlled environments don't account for certain results.
Statisticians can use three sigma calculations to set the upper and lower control limits in statistical quality control charts, which create limits for business or manufacturing processes. Here are some reasons you might use this calculation: To set control limits Related: 50 Statistics Terms To Know (With Definitions) Uses for 3 sigma calculations Three sigma follows the 68-95-99.7 rule, where 68% of the data falls within one standard deviation of the mean, 95% of the data within two standard deviations of the mean and 99.7% of the data within three standard deviations of the mean. Also referred to as the three sigma limits or empirical rule, this tool helps calculate the probability that a certain point falls within established parameters. Three sigma in statistics is a calculation that shows the bounds of data points that lie within three standard deviations from a mean in a normal distribution. In this article, we define three sigma in statistics, compare this calculation to six sigma, explain why you might use this calculation, share steps for calculating three sigma and provide an example of this calculation in a professional setting.
#Sigma symbol statistics how to#
Knowing how to calculate three sigma for a dataset can help you set control limits and produce more useful statistical reports. One of these calculations, called three sigma, can help determine if any outliers exist in a dataset when you're evaluating your collected variables.

Statisticians use a variety of calculations when gathering and interpreting data from their studies.


 0 kommentar(er)
0 kommentar(er)
